What Is A Nuclear Charge

The farther an electron moves abroad from the nucleus of an cantlet, the weaker their attraction is: discover why with our effective nuclear charge calculator.

Here you lot will learn what the effective nuclear accuse is and how to calculate information technology using Slater'southward rules. You will encounter some examples and get a quick review of the quantum theory behind atoms — and finally, yous will learn how to use our Slater'southward rules reckoner. Prepare?

A quick review of the nuclear structure

We need to take a quick look at the nuclear construction to sympathize what electron shielding is and how to calculate the effective nuclear charge.

Here are the basics of the atomic orbital model first! An atom is composed by:

A positively charged nucleus fabricated of protons and neutrons. The number of protons defines the diminutive number, uniquely identifying a chemical element.
A negatively charged electronic cloud. Each electron can exist found in a ready of defined regions of space around the nucleus called orbitals.

🙋 Breakthrough physicist hither: orbitals are solutions to the Schrodinger equation, which describes the position of an electron in space and time — just recollect, electrons are neither particles nor waves! Wavefunctions are complex quantities (in mathematical language) and bear no physical meaning: we need to accept their squared modulus that, according to the rules of breakthrough mechanics, is proportional to the probability of finding an electron in a given set of coordinates.

An orbital is described by a set of discrete integer numbers called the quantum numbers. That's why we speak of quantized — "quanta" is a Latin word for "discrete quantity". Let'south discover them:

The principal quantum number, $northward$ , which gives an indication on the distance of the electron from the nucleus. The smaller the number, the closer the electron. The value for $n$ can be whatever integer, positive value:

$northward = 0,1,2,3,\ldots$ .
The azimuthal quantum number, $50$ , which describes the shape of the region where it is possible to find the electron. Its values are related to the value of $n$ , being the integer numbers from $0$ to $n-1$ :

$fifty=0,one,\ldots,n-1$ .
The magnetic quantum number, $1000$ , which is associated with the orientation of the orbitals in space. Information technology varies according to the value of $l$ :

$m= -50,\ -fifty+ane,\ \ldots,\ 50-one,\ l$

Electrons with equal $n$ and $l$ but different values of $m$ have identical energy: nosotros telephone call the respective orbitals degenerate.

Each orbital is defined by a unique set of quantum numbers and tin host at virtually two electrons, one for each value of spin — another breakthrough property that can assume one of two values, namely spin upward or spin down.

Nosotros need to take a closer expect at the various orbitals to understand how to calculate the effective nuclear charge. Let'due south proceed in order with the breakthrough numbers, starting with the electronic shell closest to the nucleus.

For $n=1$ , the other breakthrough numbers are $l=0$ and $m=0$ . At that place is a single orbital, called $1s$ , with a spherical shape.
For $northward=two$ at that place are two possible values for $l$ : $l=0$ and $l=ane$ .
- For $50=0$ , $m=0$ too, and we get another spherical orbital, $2s$ .
- For $l=1$ there are three possible values of $m$ : $m=-1,0,+one$ . We call these orbitals $2p$ , and to distinguish the three orientations we add together a coordinate to them: $2p_x$ , $2p_y$ , and $2p_z$ . Instead of spherical, they have a dumbbell shape.
For $north=three$ we have the same orbitals we've just met, with the improver of the ones associated to $50=ii$ , for which $1000$ can assume five different values: $grand=-2,-one,0,1,ii$ . These are the $3d$ orbitals, and they assume various shapes. Our favorite of these shapes is a donut with a pear on each side.
For $n=iv$ we add together another set of orbitals, the $4f$ . They are described by the set of quantum numbers $n=4$ , $fifty=3$ , and $thousand=-3,-2,-1,0,1,ii,3$ — for a total of seven orbitals. Their shapes are even more than circuitous than the one of the $d$ orbitals.

Going upward with the value of $n$ , nosotros would meet even more complex orbitals, like $g$ , merely they don't appear in the elements we know at this time: talking of them would be meaningless!

Shape of orbitals — The shape of some of the diminutive orbitals. In the first line, the $1s$ orbital and its spherical shape. Notice also the minor size compared to the others: information technology is in the vicinity of the nucleus. In the second row, there are the $2p$ orbitals, with their three orientations. Finally, in the bottom row, you can come across the five shapes of the $3d$ orbitals.

The electron configuration

It is possible to identify each chemical element using its electron configuration. This is a style to specify the occupation of the orbitals, progressively filling the periodic tabular array.

Writing the electron configuration for an element is relatively simple — it gets challenging only for heavier elements that start to misbehave. Permit'due south take a look at the configuration for hydrogen:

$\text{H}=1s^1$

Hydrogen to a higher place has a single electron in the showtime shell. On the other paw, helium has a full get-go beat out with 2 electrons. Its configuration is:

$\text{He}=1 s^{2}$

It goes on like this, following the progression of the orbitals dictated by the following scheme:

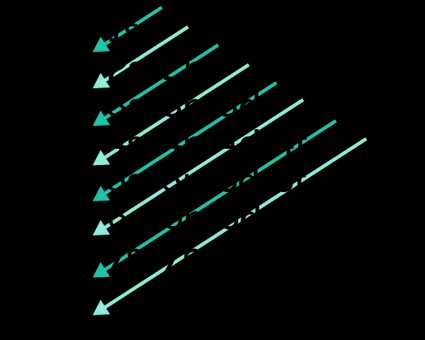
Order of occupation in orbitas — Visual representation of the occupation order of orbitals.

Follow the blue arrow from peak to bottom, writing down the orbitals in the orders they are crossed. Remember the number of electrons hosted in each shell:

$s\rightarrow 2$
$p\rightarrow 6$
$d \rightarrow 10$
$f \rightarrow 14$

Permit'south try with a heavier element, tellurium. Its atomic number is 52, which is too the number of electrons we demand to fit in the configuration.

$\brainstorm{gather*} \footnotesize 1s^2,\ 2s^2,\ 2p^6,\ 3s^2,\ 3p^half-dozen,\ 4s^2, \\ \footnotesize 3d^{x},\ 4p^6,\ 5s^ii,\ 4d^x,\ 5p^4 \end{assemble*}$

Later on you filled the electron configuration following the graphic dominion, you tin rewrite it in the most intuitive order:

$\begin{gather*}\footnotesize 1s^2,\ 2s^2,\ 2p^6,\ 3s^ii,\ 3p^half dozen,\ 3d^{10},\\ \footnotesize 4s^ii,\ 4p^6,\ 4d^{x},\ 5s^2,\ 5p^four \end{assemble*}$

That's how they are unremarkably constitute in textbooks, online, and also on our effective charge figurer.

🔎 Yous tin can see that the electron configuration of heavy elements gets a little cumbersome. Chemists establish a mode to make it easier to write and retrieve! You can employ as reference the electron configuration of noble gases and start writing the configuration from the final 1 in the periodic table, indicating it with the symbol of the chemical element in square brackets. The electron configuration of the Tellurium would exist
$\text{Te}=\left[\text{Kr}\right],\ 4d^{10},\ 5s^ii,\ 5p^4$ . Easier, isn't it?

What is electron shielding?

Electrons feel the attraction of the nucleus since they accept opposite charges. However, merely a single electron would feel the attractive force in its entirety. For every added electron sharing the same orbital or occupying lower energy orbitals, the negative charge of those particles adds a repulsive component, which contributes to the shielding of the nucleus' electrostatic interaction.

🔎 The methods explained hither are approximations that don't take into business relationship the position of the electrons and other factors. Withal, they fit the observed data.

What is the effective nuclear charge?

Nosotros need to understand first what is the nuclear charge. It is, straightforwardly, the charge of the nucleus in units of unproblematic charge, the accuse of electrons and protons (with opposite sign). The nuclear charge $Z$ thus coincides with the diminutive number. Without electrons, that would be the potential energy centered in the nucleus.

When we consider the repulsive interaction of other electrons, nonetheless, nosotros run across that the further we get from the nucleus, the lower the charge felt past an electron. We need to talk of effective nuclear charge. Nosotros denote it by $Z_\text{eff}$ .

For the offset electron around the nucleus, the constructive nuclear charge equals the nuclear accuse: $Z_\text{eff} = Z$ .

The value of $Z_\text{eff}$ then decreases approaching $one$ for an space altitude from the nucleus. This is the value of the potential energy experienced past the last electron added to the shell.

The effective nuclear charge has some distinctive trends beyond the periodic table. It increases following the groups from left to right, decreasing descending into the periods. The ratio ${Z_\text{eff}}/{Z}$ is smaller for the elements in the showtime grouping, decreasing for heavier elements (where the larger amount of electrons has a more substantial shielding effect).

How to calculate the effective nuclear charge: What are Slater'due south rules?

At present that you know what the effective nuclear accuse is, it'southward time to learn how to summate it. To do this, allow us to introduce Slater's rules. The concept at the core is that to calculate the constructive nuclear charge we need to compute the overall contribution of the shielding electrons.

Slater's rules need the consummate electron configuration of an element to be applied. We then choose an electron belonging to a specific orbital. At this indicate, we have a few different paths that tell us the shielding contribution of each electron in the configuration.

The electrons in orbitals to the correct of the chosen i give a nix contribution to the shielding.
If you chose an electron from a $p$ or an $s$ orbital, with principal quantum number $north=N$ , so:
- Electrons from orbitals with the same chief quantum number take a shielding factor of $0.35$ apart from the electrons in $1s$ , which shield $0.30$ .
- Electrons from orbitals with $n=Due north-1$ shield $0.85$ .
- Electrons coming from orbitals with $n=N-2$ or less shield $1.00$ as they are close to the nucleus.
If y'all chose an electron from an orbital with $l$ associated to $d$ or $f$ , and again $north=N$ , then:
- Electrons from orbitals with $n=North$ , and equal or bigger $l$ (following $south<p<d<f$ ) shield $0.35$ .
- Electrons from orbitals with $n+N$ but smaller $l$ than the one of the called electron shield $1.00$ .
- All other electrons from orbitals with $north<North$ shield $1.00$ .

💡 When choosing the electron, it's not essential to specify which position in the orbital we are because: the shielding effect is not affected by degeneracy.

How exercise we calculate the effective nuclear charge, then? Each shielding gene is multiplied by the number of electrons in the related orbitals, remembering to decrease ane when information technology comes to the orbital to which the chosen electron belongs. The resulting contributions are summed.

The resulting shielding is called $\sigma$ and is used to calculate $Z_\text{eff}$ through:

$Z_\text{eff}=Z-\sigma$

🙋 In that location is an exception! Hydrogen, having a single electron, has effective nuclear charge equal to the nuclear charge — that poor electron can't shield itself!

Example of how to calculate the constructive nuclear charge

Permit's choose an element and an orbital. Selenium and $3p$ , you say? That's what we were thinking as well!

This is the electron configuration of selenium, with the chosen orbital highlighted:

$\footnotesize 1s^{2}, 2s^{2}, 2p^{half-dozen}, 3s^{two}, \textbf{3p}^\textbf{6}, 3d^{10}, 4s^{2}, 4p^{iv}$

Ignore the orbitals to the right!

$\footnotesize 1s^ii, 2s^2, 2p^half dozen, 3s^2, \textbf{3p}^{\textbf{6}}, \sout{3d^{10}},\sout{4s^ii}, \sout{4p^4}$

We chose a $p$ electron, and information technology's time to employ the appropriate Slater's rules. There are $vii$ other electrons in the same grouping, with $northward=iii$ ; each contributes with $0.35$ . In the orbitals with $north=2$ , $2s$ , and $2p$ , there are $8$ electrons, which contribute individually with $0.85$ . Lastly, with $n=iii-2=ane$ , we have the two electrons in $1s$ , which contribute with a full $1.00$ each.

Let's sum up the diverse contributions then:

$\begin{marshal*} \small \sigma & =7\cdot 0.35+8\cdot 0.85+2\cdot 1.00 \\ & =xi.25 \end{align*}$

Selenium has a nuclear charge of $Z=34$ . The effective nuclear charge is obtained past subtracting from $Z$ the value of shielding $\sigma$ :

$\small Z_\text{eff} = 34-eleven.25=23.75$

How to apply our effective nuclear accuse reckoner?

First thing, choose an element from the list. They are in order of increasing atomic number. Its electron configuration will appear but beneath. Choose the desired electron from the configuration and input the advisable quantum numbers.

✅ You can't become things incorrect with this figurer. If the chosen main quantum number or the azimuthal breakthrough number is not available in the electron configuration, we will terminate you until you insert a correct set!

At the bottom of the calculator, you volition observe the values of the full shielding and of the constructive nuclear charge $Z_\text{eff}$ .

A final review!

This is all we needed to say about this topic. Now you should know how to summate $Z_\text{eff}$ without whatever difficulty, but here is a quick refresher:

Choose an electron from the electron configuration.
Utilize Slater's rules to calculate the full shielding.
Remember to ignore electrons from higher orbitals.
To calculate the constructive nuclear charge, subtract the shielding from the nuclear charge.

That's it! If you want to learn more than virtually diminutive properties, check out our electronegativity estimator, the radioactive decay estimator, or visit the chemistry page at omnicalculator.com!

FAQ

What are Slater's rules?

Slater'southward rules are a prepare of rules used in concrete chemical science to calculate the effective nuclear charge experienced by an electron around a nucleus. The rules assign a specific value of shielding to each electron according to its orbital.

Check out the Slater's rule calculator on omnicalculator.com to discover more about it!

How do I calculate the effective nuclear charge?

To calculate the effective nuclear charge:

First, compute the overall shielding upshot of the electrons orbiting the nucleus.
Subtract this value from the nuclear accuse (equal to the number of protons of the element).
Remember that the value of the effective nuclear charge depends on the orbital you are using in the calculations, since outer electrons don't contribute to the shielding!

What is the trend of the effective nuclear accuse?

The effective nuclear charge experienced by the concluding electron in the negatively charged shell decreases as the period (the rows of the periodic tabular array) increases. This is because a complete shell has been added below it (and co-ordinate to Slater'southward rules, the contribution to the shielding is higher), increasing the distance from the nucleus. The constructive accuse increases within the aforementioned period because the contribution to the shielding for orbitals with equal n is less pregnant.

What is the effective nuclear charge for neon?

Because the last electron in the electron cloud of neon, in the orbital 2p, we accept vii electrons contributing 0.35 to the shielding. We then add the contribution of the two electrons in the orbital 1s with cistron 0.85.

The full shielding is 7×0.35 + 2×0.85 = 4.15, and the effective nuclear charge is 10 − 4.fifteen = 5.85.

Cull an diminutive species

Select an electron from the electron configuration:
1s1

Electron Selection

Principal quantum number (n)

Azimuthal quantum number (l)

Results

Y'all chose an electron in the orbital 1s.

Value of the shielding: 0.00

This figurer implements Slater'south rules. Other methods may return slightly different results.

Air-fuel ratio (AFR) Arrhenius equation Diminutive mass … 32 more